らちょです。今回は固有ベクトルや対角化行列についてのお話です。
線形代数学である正方行列から固有値を算出し、固有ベクトルを求め、直行行列を作り、対角化行列を求める問題は線形代数学を履修した学生さんなら一度は見たことがあると思います。
さて、今回の議論として、直交行列を求める際に固有ベクトルを並べるのですが、皆さんは並べ方の順番について気になったことはないでしょうか?実際に計算すると、固有ベクトルの値が変わったり、変わらなかったりするので、それが一体何を意味しているのか解説していこうと思います。
具体的な例として今回は

の行列について対角化を考えます。
固有値を求める計算は省きますが、この行列の固有値はλ=3,6と算出されます。
λ=3のとき、固有ベクトルは
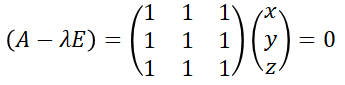
を解いて、

より、

が固有ベクトルのひとつであることが求められます。
同様にして、λ=6のとき、固有ベクトルは
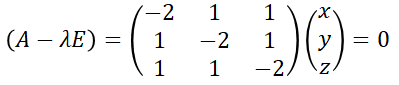
を解いて、

より、

が固有ベクトルの一つであることが求められます。
三次元正方行列に対して、固有ベクトルが3つ求められたので、次に直交行列Pを考えていきます。今回は固有ベクトルを下記の順で並べます。この時、どの固有ベクトルがどの固有値によるものなのか確認しておいてください。今回はλ=3,3,6の順番です。

これらのベクトルから正規直交基底を計算します。
正規直交基底の求め方は下記のサイトをご覧ください。
シュミットの直交化法とは:正規直交基底の具体的な求め方 | 趣味の大学数学 (math-fun.net)
すると、直交行列Pは

となる。
最後に、対角化行列Dを求めると、具体的な計算は省きますが、

より、

となり、対角化が完了しました。
先ほど、固有ベクトルに由来する固有値が3,3,6であったので、対角化行列を見ると、その並びになっていると思います。
実際に、固有値λ=3,6,3の並びで固有ベクトルを並べると、

となり、対角化行列としては、

として求められます。
以上の結果から固有ベクトルの順番によって対角化行列が異なることが分かりました。
ただし、対角化の元々の特徴としては、各ベクトルが一つの成分で表されることであり、DとD’はy軸とz軸を入れ替えただけであり、図形的な意味合いや本質的な部分は一緒です。なので、教科書や演習の答えと違っているからといって焦らないようにしましょう。
最後に今回のまとめです。
・固有値α、β、γに由来する順で固有ベクトルを並べ、対角化行列を求めた際、その対角化行列Dは必ず、
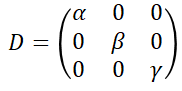
となる。
・固有ベクトルの順番を入れ替えても、対角化行列は異なるが、図形的な意味はx、y、z軸が入れ替わるだけ。
・対角化行列の検算に使える。そもそも、直交行列を計算しなくても対角化行列は求められる!
以上、らちょでした。
こちらも併せてご覧ください。https://rikedan-blog.com/?p=229




コメント